https://codeforces.com/contest/1187/problem/E
항상 궁금했던 그래프+dp 유형. editorial피셜로 기본문제라고 한다.
https://suuntree.tistory.com/126?category=805933
트리에서 모든정점 사이즈 선형시간에 구하는 법
<문제설명>
트리가 주어진다. 임의의 정점 하나를 선택한다. 그 정점을 루트로 취급할 때 그 서브트리의 모든 정점들의 size합을 구한다. 그 값 중 최대를 구해라.

dp[u] : u를 트리의 루트로 봤을 때 모든 정점의 사이즈 합
위 예시와 같이 루트를 바꿨을 때 dp값이 바뀔 여지가 있다.
dp값이 바뀐다면 참조투명하지 않다는 것인데, rerooting 테크닉을 사용하여 이를 극복하는 것에 유념하여 보면 된다.
<풀이1>
일단 직관적으로 먼저 생각해보자.
root가 1일 때 모든 정점들의 사이즈 합 dp[1],
root가 2일 떄 모든 정점들의 사이즈 합 dp[2],
....
root가 n일 때 모든 정점들의 사이즈 합 dp[n]이라고 하면 정답은
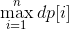
이다.
루트가 정해졌을 때 모든 정점들의 사이즈를 구하는 것은 O(n)에 전처리 할 수 있고, 그 사이즈로 같은 방법으로 O(n)에 dp배열을 채울 수 있다.
ll dfs_sz(int curr, int prv) {
sz[curr] = 1;
for (int next : adj[curr]) {
if (next == prv) continue;
sz[curr] += dfs_sz(next,curr);
}
return sz[curr];
}
ll dfs_dp(int curr, int prv) {
dp[curr] = sz[curr];
for (int next : adj[curr]) {
if (next == prv) continue;
dp[curr] += dfs_dp(next,curr);
}
return dp[curr];
}
따라서 위와같은 아이디어는 O(n*n)으로 시간초과이다. 좀더 최적화가 필요하다.
<풀이2>
루트가 u일때 모든 정점들의 사이즈 합dp[u] 를 이용해서 u에 인접한 v에 대해 dp[v]를 갱신할 수 있다.
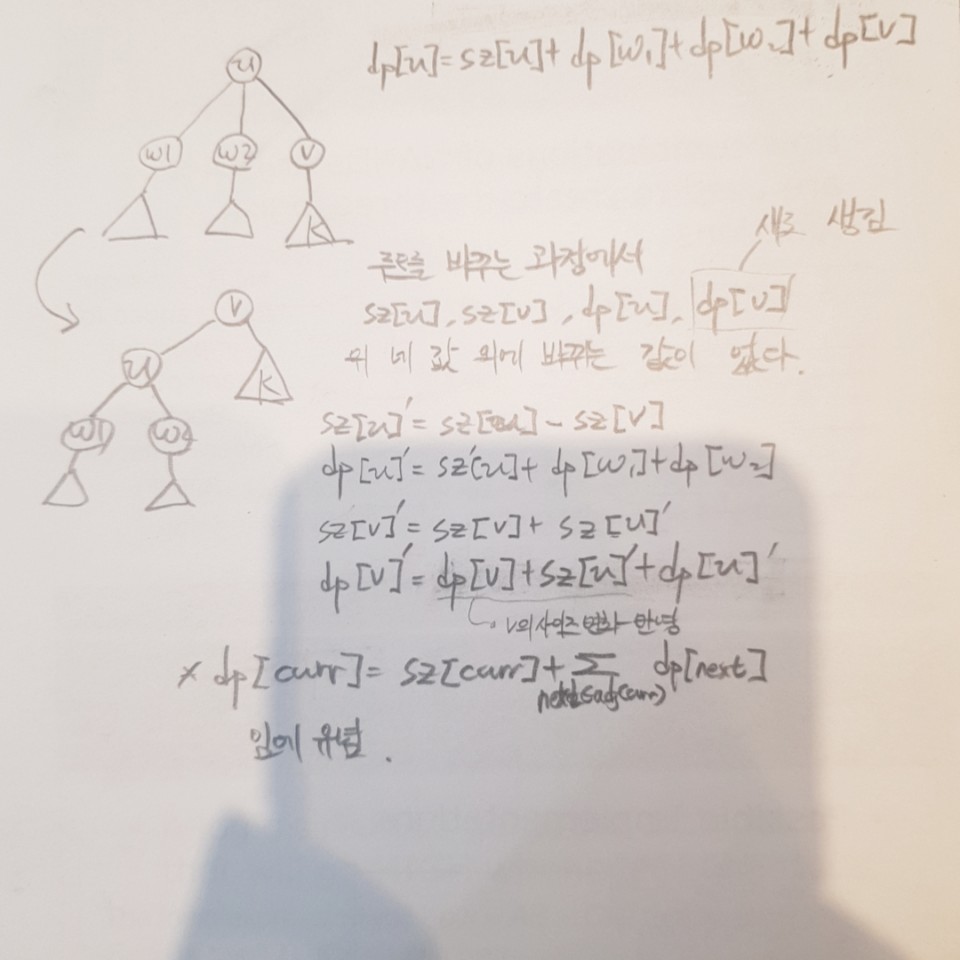
따라서 우리는 루트가 u일 때 u서브트리에 속한 모든 서브트리 사이즈 합 dp[u]를 이용해서 u에 인접한 v에 대해 dp[v]를 상수시간에 구해낼 수 있다.
시간복잡도는 size구하는 시간 + 임의값을 루트로할 때 dp 초기화 시간 + 문제 조건에 맞는 dp최댓값 구하는 시간 = 선형시간이다.
<코드>
ll n, dp[MAX], sz[MAX];
vector<int> adj[MAX];
ll dfs_sz(int curr, int prv) {
sz[curr] = 1;
for (int next : adj[curr]) {
if (next == prv) continue;
sz[curr] += dfs_sz(next,curr);
}
return sz[curr];
}
ll dfs_dp(int curr, int prv) {
dp[curr] = sz[curr];
for (int next : adj[curr]) {
if (next == prv) continue;
dp[curr] += dfs_dp(next,curr);
}
return dp[curr];
}
ll ans;
void dfs(int curr, int prv) {
ans = max(ans, dp[curr]);
for (int next : adj[curr]) {
if (next == prv) continue;
dp[curr] -= dp[next];
dp[curr] -= sz[next];
sz[curr] -= sz[next];
sz[next] += sz[curr];
dp[next] += sz[curr];
dp[next] += dp[curr];
dfs(next, curr);
//원상복구
dp[next] -= dp[curr];
dp[next] -= sz[curr];
sz[next] -= sz[curr];
sz[curr] += sz[next];
dp[curr] += sz[next];
dp[curr] += dp[next];
}
}
int main() {
FAST;
cin >> n;
for (int i = 0, u, v; i < n - 1; i++) {
cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
dfs_sz(1,0);
dfs_dp(1,0);
dfs(1, 0);
cout << ans << '\n';
}
<생각>
정점u를 루트로 했을 때 값으로 인접한 정점v를 루트로 했을 때 값을 구해낼 수 있는 경우 -> 그래프 dp, rerooting
'알고리즘 > 코드포스' 카테고리의 다른 글
| Educational #56 D - GCD counting (트리(숲) 지름, 소인수분해) (0) | 2020.03.13 |
|---|---|
| codeforces 563 div2 D - Ehab and the Expected XOR Problem (XOR, prefix xor) (0) | 2020.01.29 |
| codeforces 614 div2 C - Neko's maze game (발상) (0) | 2020.01.20 |
| Educational codeforces #80 D - Minimax Problem(이분탐색, 비트마스크) (0) | 2020.01.17 |
| codeforces 613 div2 D - Dr. Evil Underscores (분할정복) (0) | 2020.01.11 |