https://codeforces.com/contest/1173/problem/D
정확하지 않은 잘못된 점화식을 쓰려다 실패
<문제설명>
최대 2e5의 정점 n개를 갖는 트리가 주어진다. 정점을 원위에 일정한 간격으로 배치했을 때 간선이 교차하지 않는 경우의 수를 구하라.
n=4, edge = {(1,2), (1,3), (2,4)}인 경우 8. 아래 그림 참조
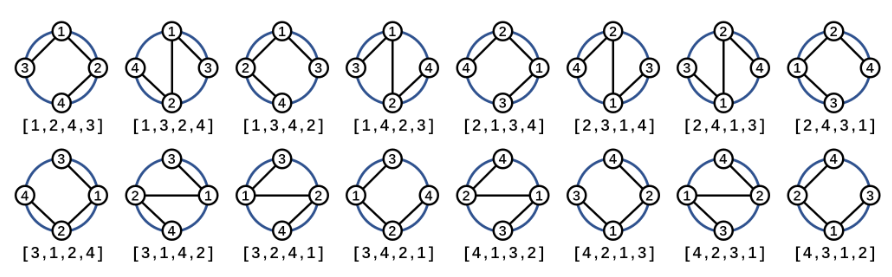
<풀이>
원의 맨 위를 1로 고정(전체드리의 루트 고정)시킨 후 경우의수를 구해서 마지막에 n을 곱하자
f(u) : u를 루트로하는 서브트리를 간선이 교차하지 않도록 배치하는 경우의 수
(각각의 자식노드를 루트로 하는 서브트리(sub(v))를 비어있는 원 위에 순서대로 배치하면 된다.
이 때, 각각의 칸 안에도 sub(v)의 루트와 그 자식들이 순서대로 배치돼야 한다. )

u가 루트인 경우는 자식수만큼 칸을 나누면 되지만, u가 루트가 아닌 경우엔 자기 자신이 들어갈 칸도 마련해야 한다는 점에 유의하자.
ans = n*f(1)
<코드>
ll n, dp[MAX], sz[MAX], ch[MAX], fac[MAX];
vector<int> adj[MAX];
void makeFac() {
fac[0] = 1;
for (ll i = 1; i < MAX; i++)
fac[i] = (fac[i - 1] * i) % MOD;
}
int makeSzch(int u, int p) {
sz[u] = 1;
for (int v : adj[u]) if (v != p) {
sz[u] += makeSzch(v, u);
ch[u]++;
}
return sz[u];
}
ll f(int u, int p) {
if (u == 1) dp[u] = (fac[ch[u]]) % MOD;
else dp[u] = fac[ch[u] + 1] % MOD;
for (int v : adj[u]) if (v != p)
dp[u] = (dp[u] * f(v, u)) % MOD;
return dp[u];
}
int main() {
FAST; cin >> n;
for (int i = 0, u, v; i < n - 1; i++) {
cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
makeFac();
makeSzch(1, 0);
cout << (n*f(1,0))%MOD << '\n';
}
<풀이2>
위 점화식을 변형하면

<코드2>
ll n, ans=1, deg[MAX];
int main() {
FAST; cin >> n;
for (int i = 0, u, v; i < n - 1; i++) {
cin >> u >> v;
ans = (ans * (++deg[u])) % MOD;
ans = (ans * (++deg[v])) % MOD;
}
cout << (ans*n)%MOD << '\n';
}'알고리즘 > 코드포스' 카테고리의 다른 글
| cf 562 div2 C - Increasing by modulo (이분탐색, 그리디) (0) | 2020.03.15 |
|---|---|
| cf 626 div2 D - present (수론, 이분탐색) (0) | 2020.03.15 |
| Codeforces #627 div3 F - Maximum white subtree (graph dp, reroot) (0) | 2020.03.14 |
| Educational #56 D - GCD counting (트리(숲) 지름, 소인수분해) (0) | 2020.03.13 |
| codeforces 563 div2 D - Ehab and the Expected XOR Problem (XOR, prefix xor) (0) | 2020.01.29 |
