공부한 블로그 : https://viruz.tistory.com/entry/EEA
Extended Euclidean algorithm
확장 유클리드 알고리즘(Extended Euclidean algorithm)은 이름에서 알 수 있듯 유클리드 알고리즘의 확장 버전이다. 기존 유클리드 알고리즘이 두 정수 $a$, $b$의 $GCD$만 구했다면, 확장 유클리드 알고리즘은..
viruz.tistory.com
다음과 같은 식을 선형 방정식이라고 한다.
ax + by = c
여기서 정수해 x,y는 c가 gcd(a,b)로 나눠지는 경우 존재한다.
gcd(a,b) = g라고 하고
ax + by = g의 값을 구하는 과정은 https://www.youtube.com/watch?v=PmwLXveLtqc참고.
유튜브 속 내용을 재귀적으로 구현하는 방법은 다음과 같다. (a,b는 양수, a>b)

점화식을 유도하는 과정은 다음과 같다.
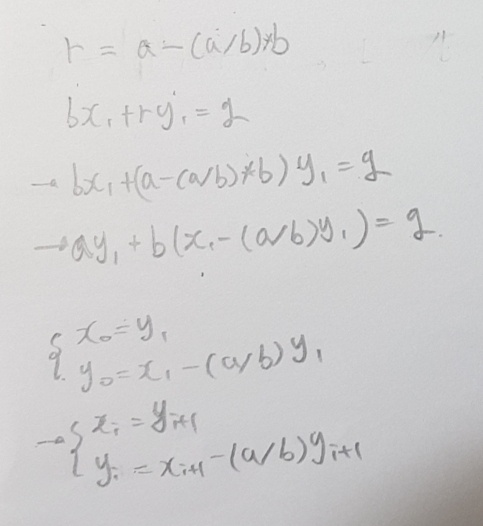
코드로 구현하면 다음과 같다.
//ax + by = gcd(a,b)
T euclid(int a, int b) { //{gcd, x, y} 튜플값 반환
if (a < b) swap(a, b); //a>b 강제
if (b == 0) return { a, 1, 0 }; //기저사례. a에 최대공약수, b엔 0들어있음.
//(xk,yk) = (1,0)
int g, x, y;
tie(g,x,y) = euclid(b, a%b);
return { g, y, x - (a / b) * y }; //x_(i) = y_(i+1), y_(i) = 위에서 적은 점화식
}
c값이나 a,b부호에 상관없이 값을 구하기 위해 잘 정리해주면 다음과 같다.
T euclid(int a, int b) {
if (a < b) swap(a, b);
if (b == 0) return { a, 1, 0 };
int g, x, y;
tie(g,x,y) = euclid(b, a%b);
return { g, y, x - (a / b) * y };
}
//a*x0 + b*y0 = c
int euclid_sol(int a, int b, int c, int &g, int &x0, int &y0){
if (a == b && b == 0)
return c!=0 ? 0 : -1; //no sol : many sol
tie(g, x0, y0) = euclid(abs(a), abs(b));
if (c % g != 0) return 0; //no sol
x0 *= c / g;
y0 *= c / g;
if (a < 0) x0 = -x0;
if (b < 0) y0 = -y0;
return 1;
}
int main() {
FAST;
int g, x, y;
int sol_state = euclid_sol(-12345, 123, 3, g, x, y);
if(sol_state==-1){
//모든 x,y에 대해 가능
}
else if (sol_state == 0) {
//근이 없음
}
else if(sol_state==1){
//최대공약수와 어떤 해 x,y값 출력
cout << g << " " << x << " " << y << '\n';
}
}
여기서 얻은 어떤 해 (x0, y0)로 모든 해를 구해보면 다음과 같다.

'알고리즘 > 메모' 카테고리의 다른 글
| 난수, 랜덤 (0) | 2020.08.28 |
|---|---|
| 머지소트 트리 (0) | 2020.06.02 |
| 1차원 직선 위 겹치는 선분들 (0) | 2020.04.05 |
| 라빈 카프, 문자열 해싱 (0) | 2020.03.21 |
| 마나커 (팰린드롬) (0) | 2020.03.20 |
