https://www.acmicpc.net/problem/8986
삼분탐색 설명
https://blog.naver.com/kks227/221432986308
unimodal 함수에 대한 설명 유념
삼분탐색에서 핵심은 이 문제를 예를들어
탐색할 큰범위가 1~1e9일때, 최소값이 들어있는 작은범위(1e3이하)를 찾아주는 것이다.
(이분탐색처럼 딱 한가지 값이 나오도록 하면 무한루프에 빠질 위험이 크다.)
블로그에선 unimodal한 함수에 대해 얘기하는데, 다른 출처에선 convex한 그래프에서 적용할 수 있다고 표현하기도 했다.
<문제설명>
1차원 축에 최대 1e5개의 전봇대가 distinct 위치에 설치돼 있다.
모든 전봇대가 같은 간격을 두고 서도록 전봇대를 움직일 때, 움직이는 횟수의 합의 최소를 구하라
<풀이>
간격이 k일때 모든 전봇대를 움직이는 횟수는 다음과 같다.
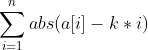
시그마 내부에 있는 함수
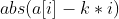
가 unimodal하므로 그 합인 모든 전봇대를 움직이는 횟수도 unimodal하다
->삼분탐색으로 최소값을 구할 수 있다.
<코드>
ll n, a[MAX];
ll f(ll k) { //간격이 x일때 움직이는 합
ll ret = 0;
for (ll i = 1; i < n; i++)
ret += abs(a[i] - k * i);
return ret;
}
int main() {
FAST; cin >> n;
for (int i = 0; i < n; i++) cin >> a[i];
if (n == 1) {
cout << 0 << '\n';
return 0;
}
ll lo = 1, hi = 1e9;
while (hi - lo >= 3) {
ll p = (lo * 2 + hi) / 3, q = (lo + hi * 2) / 3;
if (f(p) <= f(q)) hi = q;
else lo = p;
}
ll ans = 2e18;
for (int i = lo; i <= hi; i++)
ans = min(ans, f(i));
cout << ans << '\n';
}'알고리즘 > 백준 & swacademy' 카테고리의 다른 글
| BOJ 2261 - 가장 가까운 두 점 (라인스위핑) (0) | 2020.05.19 |
|---|---|
| BOJ 2568 - 전깃줄2 ( LIS, segtree ) (0) | 2020.05.14 |
| BOJ 10167 - 금광 (세그트리, 분할정복) (0) | 2020.05.11 |
| BOJ 14565 - 역원 구하기 (확장 유클리드) (0) | 2020.05.05 |
| BOJ 2472 - 체인점 (다익스트라, 좌표압축, 세그트리, 수학) (0) | 2020.04.22 |



