평면의 법선벡터를 활용해야하는 풀어볼만한 기하문제
<문제설명>
3차원 공간(r,g,b축)에 최대 100개의 점이 주어진다. 그 어떤 세 점도 한 직선 위에 있지 않고, 그 어떤 네 점도 한 평면 위에 있지 않다. 이 때, 점을 2분할 하는데, 분할방법에 따라서 점수가 달라진다. 최소 점수를 구해라
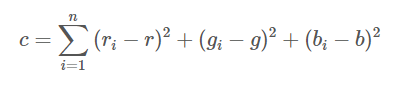
<풀이>
(접근 1)
중복되는 점이 없는 1차원 공간을 나눈다면 어떤 점을 기준으로 A,B 그룹을 나눈 후에 추가로 기준이 되는 점을 A, B그룹에 넣을 때를 비교하는 방법이 가장 빠르다.
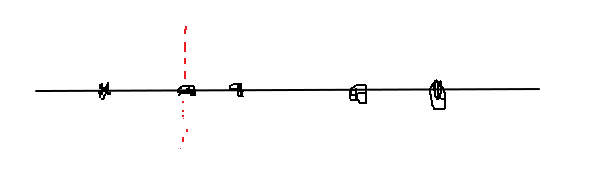
(접근 2)
어느 세 점도 같은 직선 위에 있지 않은 2차원 공간을 나눈다면, 어떤 두 점을 기준으로 A,B 그룹을 나눈 후에 추가로 기준이 되는 두 점을 A,B 그룹에 넣을 때를 비교하는 방법이 유효하다.

(최종)
3차원 공간에서도 마찬가지로, 세 점을 잡고(${O(100C3)}$), 잡은 세 점이 A,B그룹에 들어가는 모든 경우의 수를 비교해주는 방법을 사용해면 O(n^4)으로 빠듯하게 돌아간다.
P,Q,R 세 점을 지나는 평면의 법선벡터는 PQ와 PR의 외적으로 구할 수 있다.

이케저케 해서 주어진 점을 X라고 뒀을 때, OH와 HX의 내적의 부호로 A,B그룹을 나눠주면 된다.
그 후에 P,Q,R이 A,B그룹에 들어가는 8가지 경우를 모두 고려해주면 빠듯하게 돌아간다.
(아마 좀더 쉽게 나누는 법이 있을 듯 하다..)
<코드>(안다듬어서 더러움)
int n, k;
vector<T> inp;
struct item {
int cnt;
double sr, sg, sb;
double sqr, sqg, sqb;
item() {
cnt = 0;
sr = sg = sb = sqr = sqg = sqb = 0;
}
void add(T t) {
int x, y, z; tie(x, y, z) = t;
cnt++;
sr += x;
sg += y;
sb += z;
sqr += x * x;
sqg += y * y;
sqb += z * z;
}
void sub(T t) {
int x, y, z; tie(x, y, z) = t;
cnt--;
sr -= x;
sg -= y;
sb -= z;
sqr -= x * x;
sqg -= y * y;
sqb -= z * z;
}
double ret() {
if (cnt == 0) return 0;
double ret = 0;
ret += -(sr * sr / double(cnt)) + sqr;
ret += -(sg * sg / double(cnt)) + sqg;
ret += -(sb * sb / double(cnt)) + sqb;
return ret;
}
};
double dot_(T t1, T t2) {
double x[3], y[3];
tie(x[0], x[1], x[2]) = t1;
tie(y[0], y[1], y[2]) = t2;
double rst = 0;
for (int i = 0; i < 3; i++) rst += x[i] * y[i];
return rst;
}
T out_(T t1, T t2) {
double x1, x2, x3,y1,y2,y3;
tie(x1, x2, x3) = t1;
tie(y1, y2, y3) = t2;
return { x2 * y3 - x3 * y2, x3 * y1 - x1 * y3, x1 * y2 - x2 * y1 };
}
double f(vector<T>& a) {
if (a.size() == 0) return 0;
double sr = 0, sg = 0, sb = 0;
double sqr = 0, sqg = 0, sqb = 0;
for (register int i = 0,r,g,b; i < a.size(); i++) {
tie(r, g, b) = a[i];
sr += r;
sg += g;
sb += b;
sqr += r * r;
sqb += g * g;
sqb += b * b;
}
double ret = 0;
ret += -(sr * sr / double(a.size())) + sqr;
ret += -(sg * sg / double(a.size())) + sqg;
ret += -(sb * sb / double(a.size())) + sqb;
return ret;
}
int main() {
FAST; cin >> n >> k;
inp.resize(n);
for (int i = 0, r, g, b; i < n; i++) {
cin >> r >> g >> b;
inp[i] = { r,g,b };
}
if (n <= k) {
cout << "0.000000" << '\n';
return 0;
}
double ans = 1e9;
if (k == 1) {
ans = f(inp);
}
else {
for (register int i = 0; i < n; i++) for (register int j = i + 1; j < n; j++) for (register int u = j + 1; u < n; u++) {
T A = inp[i], B = inp[j], C = inp[u];
int x[3], y[3], z[3];
tie(x[0], y[0], z[0]) = A;
tie(x[1], y[1], z[1]) = B;
tie(x[2], y[2], z[2]) = C;
T AB = { x[1] - x[0], y[1] - y[0], z[1] - z[0] };
T AC = { x[2] - x[0], y[2] - y[0], z[2] - z[0] };
T H = out_(AB, AC);
double red, grn, blu, sz;
tie(red, grn, blu) = H;
sz = sqrt(red * red + grn * grn + blu * blu);
H = { red / sz,grn / sz,blu / sz };
double temp = dot_(H, A);
T X = { get<0>(H) * temp, get<1>(H) * temp, get<2>(H) * temp };
item s1, s2;
s1.cnt = 0; s2.cnt = 0;
for (register int v = 0, r, g, b, p1, p2, p3; v < n; v++) {
if (v == i || v == j || v == u) continue;
tie(r, g, b) = inp[v];
tie(p1, p2, p3) = X;
T XP = { r - p1, g - p2, b - p3 };
if (dot_(X, XP) > 0) s1.add(inp[v]);
else s2.add(inp[v]);
}
for (int q = 0; q < 8; q++) { //점A
q& (1 << 0) ? s1.add(A) : s2.add(A);
q& (1 << 1) ? s1.add(B) : s2.add(B);
q& (1 << 2) ? s1.add(C) : s2.add(C);
double t1 = s1.ret(), t2 = s2.ret();
q& (1 << 0) ? s1.sub(A) : s2.sub(A);
q& (1 << 1) ? s1.sub(B) : s2.sub(B);
q& (1 << 2) ? s1.sub(C) : s2.sub(C);
ans = min(ans, t1 + t2);
}
}
}
cout << fixed;
setprecision(6);
cout << ans << '\n';
}
'알고리즘 > 백준 & swacademy' 카테고리의 다른 글
| BOJ 20176 - Needle (FFT) (0) | 2021.01.02 |
|---|---|
| BOJ 11003 - 최솟값 찾기 (monotonic queue) (0) | 2020.08.12 |
| BOJ 7469 - K번째 수 ( 머지소트트리, pst ) (0) | 2020.06.10 |
| BOJ 17306 - 전쟁 중의 삶 (트라이, 완전이진트리) (0) | 2020.06.10 |
| BOJ 3392 - 화성지도 (세그트리 응용) (0) | 2020.06.06 |