[공업수학] 벡터의 외적
본 자료는 국립 창원대학교 메카트로닉스 공학부 학생을 대상으로 한 공업수학 수업 자료입니다. 본 자료는 수업의 교재인 공업수학I 개정3판 (고형준 외, 도서출판 텍스트북스) 의 내용을 재구성한 것으로 수업보..
pinkwink.kr
라이님의 블로그와 위 블로그에서 사진을 가져왔음을 밝힙니다.

벡터의 외적은 교환/결합법칙이 성립되지 않는다.

외적의 크기는 두 벡터가 이루는 평행사변형의 넓이이고 방향은 법선방향이다. (오른나사법칙)

외적의 결과. 맨 밑 행렬만 기억하면 된다.
코드를 짤 땐 보통 2차원 평면에서 다루기 떄문에 k성분을 0으로 두고 생각하면 되겠다.
----------------------------------
2차원 평면에서의 외적을 ccw라고 한다. 코드 이해안되면 행렬식을 보자
typedef pair<int,int> vec;
int ccw(vec a, vec b){
int x1 = a.first, y1 = a.second;
int x2 = b.first, y2 = b.second;
return x1*y2 - x2*y1;
}결과값의 부호가 외적벡터의 방향을 의미한다고 볼 수 있다.
a벡터와 b벡터가 시계방향으로 놓여있다면 양수, 시계 반대방향으로 놓여있다면 음수를 반환한다. (오른나사법칙)
두 벡터가 같은 직선 위에 놓여있을 수 있다면 0을 반환한다.
-----------------------------------
두 선분이 아래 그림과 같이 교차하는지 여부를 파악하는 로직
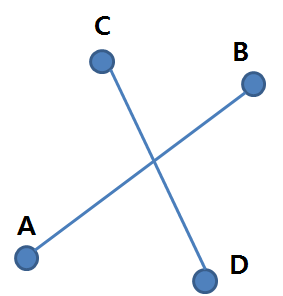
1. ABxAC 의 부호와 ABxAD의 부호가 달라야 하고, CDxCA의 부호와 CDxCB의 부호가 달라야 한다.
부호를 반환하는 ccw에 대해서
if(ccw(AB,AC)!=ccw(AB,AD) && ccw(CD,CA)!=ccw(CD,CB)) cross = true;
(교차 + 접하는 것도 허용한다면..)
2.예외처리 :
-점 C가 선분 AB위에 있는 경우, 점 D가 선분 AB위에 있는 경우,
ABxAC, ABxAD 둘 중 하나가 0이고 CDxCA의 부호와 CDxCB의 부호가 다르면 된다.
if(ccw(AB,AC)*ccw(AB,AD)==0 && ccw(CD,CA)!=ccw(CD,CB)) cross = true;
-점 A가 선분 CD에 있는 경우, 점 B가 선분 CD에 있는 경우..
ABxAC 의 부호와 ABxAD의 부호가 달라야 하고 CDxCA, CDxCB 둘 중 하나가 0이면 된다.
if(ccw(AB,AC)!=ccw(AB,AD) && ccw(CD,CA)*ccw(CD,CB)==0) cross = true;
-두 선분이 같은 직선 위에 있는 경우
if(ccw(AB,AC)==0 && ccw(AB,AD)==0) // 두 선분이 같은 직선 위에 있는 경우
겹친 선분의 전체 길이 len은
len = max({ AC, AD, BC, BD }); 이 되는데,
len<AB+CD라면 두 선분이 겹쳐있게 된다.
'알고리즘 > 메모' 카테고리의 다른 글
| 냅색, knapsack (0) | 2019.08.19 |
|---|---|
| 기하 - 두 선분 사이의 거리 (0) | 2019.08.19 |
| 2-SAT(Boolean Satisfiability) (0) | 2019.08.19 |
| 강한 연결 요소(SCC) (0) | 2019.08.19 |
| 위상정렬, DAG(Directed Acyclic Graph) (0) | 2019.08.18 |
