라이님 블로그에서 공부했음을 밝힙니다
https://blog.naver.com/kks227/220794097589
https://www.acmicpc.net/problem/11563
11563번: 연돌이와 고잠녀
첫 줄에는 신촌에 연결된 도로의 숫자 n과 안암에 연결된 도로의 숫자 m(1 <= n, m <= 2,000)이 주어진다. 이어지는 n줄에 걸쳐 신촌에 연결된 도로의 정보가 (xs, ys), (xe, ye) 형태로 주어지며(-10,000 <= xs, ys, xe, ye <= 10,000, 좌표들은 실수) 이는 (xs, ys)와 (xe, ye)를 잇는 도로가 있다는 것을 뜻한다. 이어지는 m줄에 걸쳐 안암에 연결된 도로의 정보가 (xs, ys), (xe, y
www.acmicpc.net
이 문제로 연습하면 좋다.
두 선분 사이의 거리를 구할 땐 크게 2가지 경우를 살펴보면 된다.
1.

이 경우 d = min({DA,DB}, {CA,CB}); 그냥 두 정점간 거리 중 최단 거리를 뽑아주면 된다.
2.
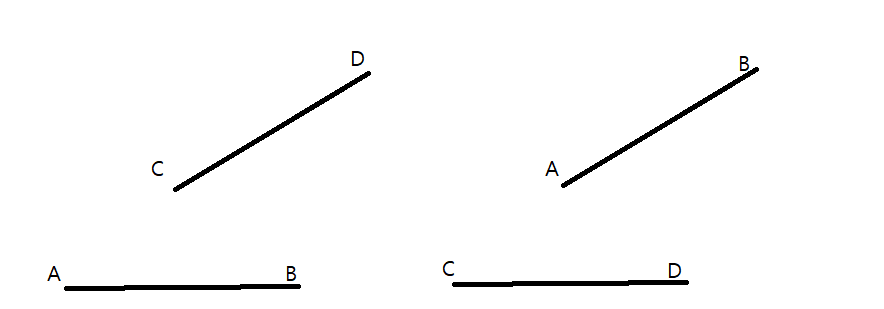
이 경우 대충 보면 d = min({dist(C, AB), dist(D,AB)}, {dist(A,CD), dist(B,CD)}); 인데,
점과 선분 사이의 거리를 보기 위해선, 예를들어 왼쪽 그림을 봤을 떄, 점 C에서 선분 AB에 내린 수선의 발 R이 선분 AB위에 있어야 한다. (점 D에서 직선 AB에 내린 수선의 발은 선분 AB 밖에 있다)
위의 조건을 만족하기 위해선, iproduct(AB,AC) > 0 && iproduct(BA,BC) > 0 이어야 한다.
왼쪽 그림을 보며 이제 점과 수선의 발 사이의 거리(점과 선분 사잉의 거리)를 구하는 법을 알아보자.
신발끈 공식 등을 이용해서 삼각형 ABC의 면적*2을 구한 후, 선분AB로 나눠주면 된다.
typedef pair<double, double> Point;
typedef Point Vec;
typedef pair<Point, Point> Road;
long double distBetweenRoad(Road r1, Road r2) {
Point A = r1.first, B = r1.second, C = r2.first, D = r2.second;
long double mn = min(min(distBetweenPoint(A, C), distBetweenPoint(A, D)),
min(distBetweenPoint(B, C), distBetweenPoint(B, D)));
long double h = 1e9;
if (innerProduct({ C.first - A.first, C.second - A.second }, { B.first - A.first, B.second - A.second })>0 &&
innerProduct({ C.first - B.first, C.second - B.second }, { A.first - B.first, A.second - B.second })>0) {
long double s = triangle(A, B, C);
h = min(h, s / distBetweenPoint(A, B) );
}
if (innerProduct({ D.first - A.first, D.second - A.second }, { B.first - A.first, B.second - A.second })>0 &&
innerProduct({ D.first - B.first, D.second - B.second }, { A.first - B.first, A.second - B.second }) >0) {
long double s = triangle(A, B, D);
h = min(h, s / distBetweenPoint(A, B) );
}
if (innerProduct({ A.first - C.first, A.second - C.second }, { D.first - C.first, D.second - C.second }) > 0 &&
innerProduct({ A.first - D.first, A.second - D.second }, { C.first - D.first, C.second - D.second }) > 0) {
long double s = triangle(A, C, D);
h = min(h, s / distBetweenPoint(C, D));
}
if (innerProduct({ B.first - C.first, B.second - C.second }, { D.first - C.first, D.second - C.second }) > 0 &&
innerProduct({ B.first - D.first, B.second - D.second }, { C.first - D.first, C.second - D.second }) > 0) {
long double s = triangle(B, C, D);
h = min(h, s / distBetweenPoint(C, D));
}
return min(mn, h);
}
'알고리즘 > 메모' 카테고리의 다른 글
| lazy propagation - 세그먼트 트리 확장 (0) | 2019.09.18 |
|---|---|
| 냅색, knapsack (0) | 2019.08.19 |
| 기하1 - 외적, 두 선분의 교차 (0) | 2019.08.19 |
| 2-SAT(Boolean Satisfiability) (0) | 2019.08.19 |
| 강한 연결 요소(SCC) (0) | 2019.08.19 |
