www.youtube.com/watch?v=6omvN1nuZMc&list=PLJN246lAkhQjX3LOdLVnfdFaCbGouEBeb&index=13
박해선 교수님의 유튜브 강의로 공부했음을 밝힙니다.
선형 회귀 모델을 훈련시키는 두 가지 방법
- 정규방정식
- 경사하강법 GD(배치, 미니배치, 확률적(stochastic))
경사하강법
특성이 매우 많고 훈련 샘플이 너무 많아 메모리에 모두 담을 수 없을 때 적합함.
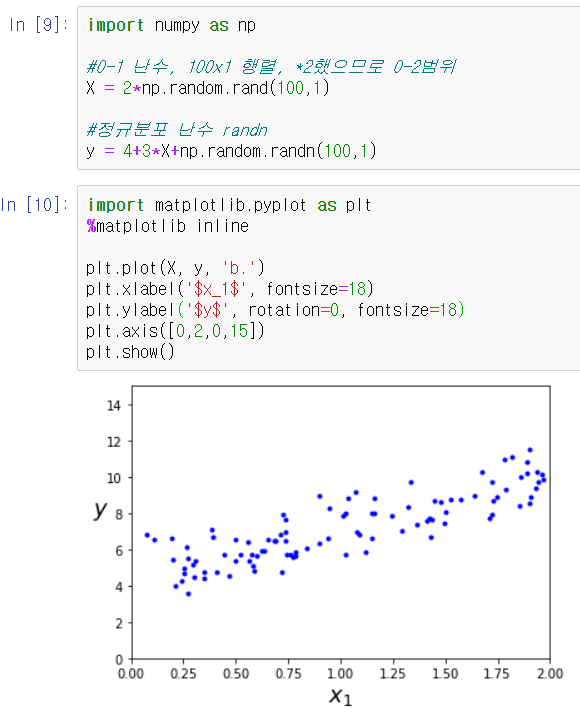
<실제 모듈 사용>
sklearn.linear_model 의 SGDRegressor을 사용하면 된다. 확률적 경사하강법(SGD)이 구현돼 있다.
from sklearn.linear_model import SGDRegressor
#learning_rate = 'invscaling' -> eta0/t**0.25, 학습률을 점점 줄여나감.
#learning_rate = 'constant' -> eta0를 계속 사용함
sgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, penalty=None, eta0=0.1, random_state=42)
sgd_reg.fit(X, y.ravel()) #2차원인 y를 1차원으로 폄
sgd_reg.intercept_, sgd_reg.coef_
#(array([4.38308587]), array([2.74583828]))
<경사하강법의 문제>

- learning rate를 적절히 정해서 발산하지 않도록, 평지에서 멈추지 않도록 해야한다.
- 지역최솟값으로 수렴하는 경우도 있겠지만, 다른 것들이 잘 갖춰져 있다면 지역최솟값도 나쁘지 않다.
- 특성이 여러 개일 때 모든 특성이 같은 스케일을 갖도록 해야 빠르게 학습할 수 있다.
<배치 경사하강법>
매 epoch마다 전체 샘플을 이용해서 단순히 경사하강법을 적용하는 방법.
1. $\hat{\theta}$를 랜덤으로 초기화.
2. 에포크 시작
- 경사하강법 수행
3. 에포크 종료


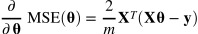

구현
eta = 0.1
n_iterations=1000
m=100
theta = np.random.randn(2,1) #가중치를 랜덤으로 초기화
for iteration in range(n_iterations):
gradients = 2/m * X_b.T.dot(X_b.dot(theta)-y)
theta = theta -eta*gradients
theta
#array([[4.41766218],
# [2.74273432]])
<확률적 경사 하강법>
SGD라고도 함.
1. $\hat{\theta}$를 랜덤으로 초기화.
2. 에포크 시작
ㅁ 훈련세트 섞기, 반복 시작
훈련 세트에서 샘플 하나 꺼내기
경사하강법 수행
모든 샘플에 대해 수행했으면 반복 종료
3. 종료
아래 코드는 랜덤하게 샘플을 꺼내긴 하지만 중복을 허용해서 m번 반복하는 것으로 퉁쳤다. 실제로 SGDRegressor에선 모든 샘플이 한 번씩은 선택되도록 구현한다.
theta_path_sgd = [] #그래프 그리기 위함
m = len(X_b)
np.random.seed(42)
n_epochs = 50
t0, t1 = 5, 50
#0.1
#5/(49*100+99+50)
def learning_schedule(t):
return t0 / (t+t1)
theta = np.random.randn(2,1) #랜덤 초기화
for epoch in range(n_epochs):
for i in range(m):
if epoch==0 and i<20:
y_predict = X_new_b.dot(theta)
style='b--' if i> 0 else 'r--'
plt.plot(X_new, y_predict, style)
random_index = np.random.randint(m)
xi = X_b[random_index:random_index+1]
yi = y[random_index:random_index+1]
gradients = 2*xi.T.dot(xi.dot(theta) - yi)
eta = learning_schedule(epoch*m+i)
theta = theta - eta*gradients
theta_path_sgd.append(theta)
plt.plot(X,y,'b.')
plt.xlabel('$x_1$', fontsize=18)
plt.ylabel('$y$', rotation=0, fontsize=18)
plt.axis([0,2,0,15])
plt.show()
<미니배치 경사하강법>
배치경사하강법과 SGD의 절충안
1. $\hat{\theta}$를 랜덤으로 초기화.
2. 에포크 시작
ㅁ 훈련세트 섞기, 미니배치 단위로 커지는 반복 시작
훈련 세트에서 샘플 미니배치 단위로 꺼내기
경사하강법 수행
모든 샘플에 대해 수행했으면 반복 종료
3. 종료
theta_path_mgd = []
n_iterations = 50
minibatch_size = 20
np.random.seed(42)
theta = np.random.randn(2,1)
t0, t1 = 200, 1000
def learning_schedule(t):
return t0 / (t+t1)
t=0
for epoch in range(n_iterations):
shuffled_indices = np.random.permutation(m)
X_b_shuffled = X_b[shuffled_indices]
y_shuffled = y[shuaffled_indices]
for i in range(0,m,minibatch_size):
t += 1
xi = X_b_shuffled[i:i+minibatch_size]
yi = y_shuffled[i:i+minibatch_size]
gradients = 2/minibatch_size * xi.T.dot(xi.dot(theta) - yi)
eta = learning_schedule(t)
theta = theta-eta*gradients
theta_path_mgd.append(theta)
theta
#array([[4.45427431],
# [2.76386051]])
<추가>

각 경사하강법 방법에 따른 최적 해를 찾아가는 모습이다.
메모리와 시간이 여유롭다면 배치 경사하강법 방법을 사용하는 것이 가장 좋다.
여유롭지 않다면 미니배치나 SGD를 사용하는 것이 좋다.
딥러닝에선 미니배치 방식을 많이 쓴다고 한다.

표를 보면 SGDRegressor에서 배치, 확률, 미니배치를 모두 지원한다고 돼 있지만 엄밀히 말해선 SGDRegressor은 확률적 경사하강법만 지원한다고 생각하면 된다.
partial_fit은 부분적 학습기능을 지원하는데, 이를 이용해서 미니배치 경사하강법을 구현할 수는 있지만, partial_fit조차도 내부에선 하나의 샘플씩 꺼내기 때문에 엄밀히 말해선 이것도 SGD이다.
'ML&DATA > 핸즈온 머신러닝' 카테고리의 다른 글
| 4 - 로지스틱 회귀, 소프트맥스 회귀 (0) | 2020.09.15 |
|---|---|
| 4 - 다항회귀, 규제 (2) | 2020.09.09 |
| 4 - 선형 회귀 (정규방정식) (0) | 2020.09.04 |
| 3 - 다중 레이블 분류, 다중 출력 분류 (2) | 2020.08.27 |
| 3 - 에러분석 (0) | 2020.08.27 |



