www.youtube.com/watch?v=6omvN1nuZMc&list=PLJN246lAkhQjX3LOdLVnfdFaCbGouEBeb&index=13
박해선 교수님의 유튜브 강의로 공부했음을 밝힙니다.
4.6 로지스틱 회귀
로지스틱 회귀 : 분류에 사용되는 회귀모델. 샘플이 특정 하나의 클래스에 속할 확률(predict_proba)을 추정한다.
소프트맥스 회귀 : 다항 로지스틱 회귀라고도 한다. 각 클래스에 속할 확률을 추정한다.
<실제 모듈 사용>
sklearn.linear_model의 LogisticRegression사용. coef_속성은 (클래스 수, 특성 수)크기의 2차원배열. intercept_속성은 클래스 수와 같은 1차원 배열
1. 로지스틱 회귀
머신러닝의 'hello world'라고 부르는 붓꽃 데이터 셋. 꽃밪침 너비/길이, 꽃잎 너비/길이를 feature로 가지고 setosa,versicolour, virginica 세가지 클래스를 갖는다.
from sklearn import datasets
iris = datasets.load_iris()
list(iris.keys())
#['data',
# 'target',
# 'frame',
# 'target_names',
# 'DESCR',
# 'feature_names',
# 'filename']
#클래스마다 50개씩의 데이터를 갖는다.
np.unique(iris.target, return_counts=True)
#(array([0, 1, 2]), array([50, 50, 50], dtype=int64))
#꽃잎 너비만 특성으로 사용 (그래프 그리기 쉽게 하기 위함임. )
X = iris['data'][:,3:]
#Iris virginica면 1 아니면 0
y = (iris['target'] == 2).astype(np.int)
X.shape #(150,1) 범위인덱스로 뽑았으므로 2차원
로지스틱 회귀 모델을 훈련. sklearn.linear_model의 LogisticRegression 사용
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(random_state=42)
log_reg.fit(X,y)
사용법
log_reg.predict_proba(X_new) #X_new의 로지스틱 회귀 결과 확률벡터를 반환함
log_reg.predict(X_new) #X_new의 클래스 예측벡터 반환
사용예
꽃잎의 너비가 0~3cm인 꽃에 대해 모델의 추정 확률 계산
X_new = np.linspace(0,3,1000).reshape(-1,1)
y_proba = log_reg.predict_proba(X_new) #추정확률 y_proba에
plt.plot(X_new, y_proba[:,1], 'g--', linewidth=2, label ='Iris virginica')
plt.plot(X_new, y_proba[:,0], 'b--', linewidth=2, label ='not Iris virginica')
plt.legend()
2. 소프트맥스 회귀
사용할 데이터
X = iris['data'][:,(2,3)] #꽃잎 길이, 꽃잎 너비
y = iris['target'] #3개의 붓꽃
X.shape #(150,2)
소프트맥스 회귀 모델을 훈련. LogisticRegression의 multi_class옵션을 'multinomial'로 설정하여 사용
softmax_reg = LogisticRegression(multi_class = 'multinomial', C=10, random_state=42)
softmax_reg.fit(X,y)
사용법
softmax_reg.predict([[5,2]])
#array([2])
softmax_reg.predict_proba([[5,2]])
#array([[6.38014896e-07, 5.74929995e-02, 9.42506362e-01]])
<로지스틱 회귀>
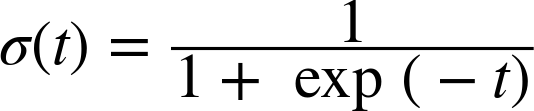
로지스틱 회귀모델에서 어떤 샘플에 대한 확률 추정식은 위 시그모이드 함수를 사용해서 정의한다.

샘플의 추정라벨 $\hat{y}$은 추정확률$\hat{p}$이 0.5이상이면 양성, 0.5미만이면 음성이다.

모델을 훈련시키기 위한 비용함수를 알아보자.
하나의 샘플에 대한 비용함수는 다음과 같다. 라벨이 1인 경우 확률이 0에 가까울수록 큰 비용 발생하고, 라벨이 0인 경우 확률이 1에 가까울수록 큰 비용이 발생한다는 의미를 갖는다.

정리하면 경우에 따른 교차 엔트로피 오차라고 할 수 있는 것 같다.
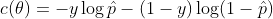
전체 훈련세트에 대한 비용함수는 모든 훈련샘플의 비용을 평균한 것이다. 이걸 로그손실이라고 한다.

미분해서 경사하강법에 사용하면 된다.

<소프트맥스 회귀>
- $k$ : 클래스 수
- $s(x)$ : 샘플 $x$에 대한 각 범주의 점수를 담고 있는 벡터
- $\sigma(s(x))_k$ : 이 샘플이 범주 $k$에 속할 확률
샘플 $x$가 주어지면 소프트맥스 회귀 모델이 각 클래스 $k$에 대한 점수 $s_k(x)$를 계산하고, 그 점수에 소프트맥스 함수를 적용하여 각 범주별 속할 확률을 추정한다.


추정라벨 $\hat{y}$는 추정확률$\hat{p}_k이 가장 높은 클래스를 선택함

모델을 훈련시키기 위한 비용함수를 알아보자.
교차(크로스) 엔트로피 오차를 사용한다. suuntree.tistory.com/299
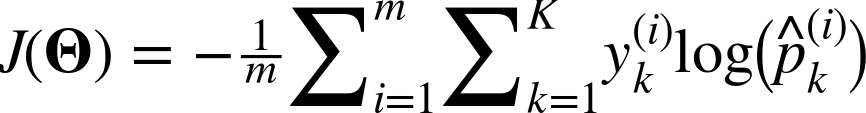
역시 미분해서 경사하강에 사용하면 된다.

'ML&DATA > 핸즈온 머신러닝' 카테고리의 다른 글
| 5. SVM - 선형분류 (0) | 2020.09.28 |
|---|---|
| 4 - 정리, 연습문제 (0) | 2020.09.18 |
| 4 - 다항회귀, 규제 (2) | 2020.09.09 |
| 4 - 선형회귀 (경사하강법) (0) | 2020.09.04 |
| 4 - 선형 회귀 (정규방정식) (0) | 2020.09.04 |



